Psychic Origami

stochastic optimisation

As we often just want a good solution fairly quickly we can turn to stochastic optimisation methods. We take randomly generated routes through the cities and incrementally improve/change them in some fashion to search for a better route. How these changes are made depends on the algorithm being used, but there are a couple of simple approaches we can take, that I will outline here:

• swapping the position of two cities on a route
• reversing the order of an entire section of a route

These simple operators - so called as they “operate” on a route to create a new one - will form the initial basis of my code. There are more complex operators, but for simplicity I shall not talk about them here.

finally on with some code....

I will be using standard Python lists to represent a route (or tour as I refer to it in my code - a name borrowed from graph theory) through a collection of cities. Each city will simply be assigned a number from 0 to N-1 (where N is the number of cities) and therefore our list of cities will be a list of unique numbers between 0 and N-1.

We also need to specify a “distance matrix” that we can use to find out the distance between two cities. To generate a distance matrix for a set of x,y co-ordinates the following will do nicely:

def cartesian_matrix(coords):
    '''create a distance matrix for the city coords
      that uses straight line distance'''
    matrix={}
    for i,(x1,y1) in enumerate(coords):
        for j,(x2,y2) in enumerate(coords):
            dx,dy=x1-x2,y1-y2
            dist=sqrt(dx*dx + dy*dy)
            matrix[i,j]=dist
    return matrix

cartesian_matrix() takes a Python list of (x,y) tuples and outputs a Python dictionary that contains the distance between the distances between any two cities:

>>> matrix=cartesian_matrix([(0,0),(1,0),(1,1)])
>>> print matrix
{(0, 1): 1.0, (1, 2): 1.0, (0, 0): 0.0, (2, 1): 1.0,
(1, 1): 0.0, (2, 0): 1.4142135623730951, (2, 2): 0.0,
(1, 0): 1.0, (0, 2): 1.4142135623730951}
>>> print matrix[1,2]
1.0

Where matrix[1,2] gives the distance between city number 1 and city number 2. In our case this is the same as matrix[2,1], but for some TSP's it may not be (for example if there is a one way street between locations/cities that means we have to take a long way round when going in one direction).

In addition to generating the distance matrix we will probably also want to read the city co-ordinates from a text file (one x,y per line):

def read_coords(coord_file):
    coords=[]
    for line in coord_file:
        x,y=line.strip().split(',')
        coords.append((float(x),float(y)))
    return coords

That should be sufficient for generating distance matrices for now. On real world problems generating a distance matrix may be more involved - you might need to take map data and calculate what the actual distance by road between any two cities is. This process can be done offline, before we start optimising our routes and is a subject for another time.

Ok, so now we can read in a list of cities from a file and generate our distance matrix. What next? Well it would be good if we knew how long a route was:

def tour_length(matrix,tour):
    total=0
    num_cities=len(tour)
    for i in range(num_cities):
        j=(i+1)%num_cities
        city_i=tour[i]
        city_j=tour[j]
        total+=matrix[city_i,city_j]
    return total

Where matrix is a distance matrix and tour is a list of cities (as integers).

implementing the operators

I am going to implement the two operators as generator functions, that will return (in a random order) all of the possible versions of a route that can be made in one step of the operator. By using a generator function we can assess each different possibility and perhaps decide to not generate any more variations - which saves us the overhead of generating all of the combinations in one go. Both operators rely on the following generator function:

def all_pairs(size,shuffle=random.shuffle):
    r1=range(size)
    r2=range(size)
    if shuffle:
        shuffle(r1)
        shuffle(r2)
    for i in r1:
        for j in r2:
            yield (i,j)

Which will generate all pairings of the numbers from 0 to size as (i,j) tuples in a random order (needs the random module imported to work).

So each operator then looks like:

def swapped_cities(tour):
    '''generator to create all possible variations
      where two cities have been swapped'''
    for i,j in all_pairs(len(tour)):
        if i < j:
            copy=tour[:]
            copy[i],copy[j]=tour[j],tour[i]
            yield copy

and

def reversed_sections(tour):
    '''generator to return all possible variations
      where the section between two cities are swapped'''
    for i,j in all_pairs(len(tour)):
        if i != j:
            copy=tour[:]
            if i < j:
                copy[i:j+1]=reversed(tour[i:j+1])
            else:
                copy[i+1:]=reversed(tour[:j])
                copy[:j]=reversed(tour[i+1:])
            if copy != tour: # no point returning the same tour
                yield copy

Note I'm using copy=tour[:] to duplicate the route, rather than copy=list(tour) (or similar). Although I am currently using a Python list to represent a tour I may in the future want to use something else that is merely “list-like”, in which case I could just override __getitem__ to return an object of the appropriate type.

Using both operators looks like:

>>> for tour in swapped_cities([1,2,3]):
...     print tour
...
[3, 2, 1]
[2, 1, 3]
[1, 3, 2]
>>> for tour in reversed_sections([1,2,3]):
...     print tour
...
[3, 2, 1]
[2, 1, 3]
[2, 3, 1]
[3, 1, 2]
[1, 3, 2]

As you can see reversed_sections gives us a lot more possibilities - even with only 3 cities. I'll compare how these two operators stack up in the next part of the series.

additional code

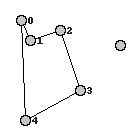
The last piece of utility code for today generates a .png of a route overlaid on top of the city co-ordinates (using PIL):

def write_tour_to_img(coords,tour,img_file):
    padding=20
    # shift all coords in a bit
    coords=[(x+padding,y+padding) for (x,y) in coords]
    maxx,maxy=0,0
    for x,y in coords:
        maxx=max(x,maxx)
        maxy=max(y,maxy)
    maxx+=padding
    maxy+=padding
    img=Image.new("RGB",(int(maxx),int(maxy)),color=(255,255,255))

    font=ImageFont.load_default()
    d=ImageDraw.Draw(img);
    num_cities=len(tour)
    for i in range(num_cities):
        j=(i+1)%num_cities
        city_i=tour[i]
        city_j=tour[j]
        x1,y1=coords[city_i]
        x2,y2=coords[city_j]
        d.line((int(x1),int(y1),int(x2),int(y2)),fill=(0,0,0))
        d.text((int(x1)+7,int(y1)-5),str(i),font=font,fill=(32,32,32))


    for x,y in coords:
        x,y=int(x),int(y)
        d.ellipse((x-5,y-5,x+5,y+5),outline=(0,0,0),fill=(196,196,196))
    del d
    img.save(img_file, "PNG")

Which produces output along these lines:

conclusion

Well that's it for part one. At this point you can create a distance matrix, see how long a route is, create a few different variations of a route and create an image of a route. The missing part is being able to generate a good route. I'll save that for the next part, where I'll discuss the simplest stochastic optimisation method: Hill-climbing.

source-code

Full source-code is available here as a .tar.gz file. I've included some unit tests which can be run using nosetests.

references

1. http://www.tsp.gatech.edu/
2. http://mathworld.wolfram.com/NP-HardProblem.html
3. http://en.wikipedia.org/wiki/Stochastic_optimization